Verschlüsselungsverfahren im Überblick
Unter Verschlüsselung (Chiffrierung) versteht man ein Verfahren, bei dem Klartext mithilfe eines Schlüssels in eine unverständliche Zeichenfolge übersetzt wird. Im besten Fall ist der Inhalt des so gewonnenen Geheimtextes (Chiffrats) nur dem zugänglich, der die Chiffrierung mithilfe des Schlüssels wieder rückgängig machen kann. Die Begriffe „Klartext“ und „Geheimtext“ können dabei als historisch gewachsen betrachtet werden. Außer auf Textnachrichten lassen sich moderne Verschlüsselungsverfahren auch auf andere elektronisch vorliegende Informationen wie Sprachnachrichten, Bilddateien oder Programmcode anwenden.
Verschlüsselung wird eingesetzt, um Dateien, Laufwerke oder Verzeichnisse vor unerwünschten Zugriffen zu schützen oder Daten vertraulich zu übermitteln. Bereits in der Antike kamen einfache Verschlüsselungsverfahren zum Einsatz, die sich in erster Linie auf eine Codierung der zu schützenden Informationen beschränkten. Dabei werden einzelne Zeichen des Klartextes, Wörter oder ganze Sätze innerhalb der Botschaft umsortiert (Transposition) oder durch alternative Zeichenkombinationen ersetzt (Substitution).
Um einen derart verschlüsselten Text anschließend wieder decodieren zu können, muss der Empfänger die Regel kennen, nach der der Text chiffriert wurde. Permutationen im Rahmen von Transpositionsverfahren werden in der Regel anhand einer Matrix vorgenommen. Um einen transponierten Geheimtext in Klartext umschreiben zu können, muss die Transpositionsmatrix bekannt sein oder rekonstruiert werden. Substitutionsverfahren stützen sich auf eine tabellarische Zuordnung von Klartextzeichen und Chiffren in Form eines geheimen Codebuchs.
Eines der ersten und einfachsten Verschlüsselungsverfahren dieser Art geht auf Gaius Julius Cäsar zurück. Die sogenannte Cäsar-Verschlüsselung basiert auf monoalphabetischer Substitution. Um seine militärische Korrespondenz vor feindlichen Spionen zu schützen, verschob der gewiefte Feldherr die Buchstaben seiner Wörter um drei Schritte im Alphabet. Das Ergebnis war folgendes:
Die Anzahl der Schritte, um die die Zeichen verschoben werden, kann bei dieser Art der Chiffrierung als Schlüssel betrachtet werden. Dieser wird nicht als Zahl angegeben, sondern mit dem entsprechenden Buchstaben im Alphabet. Eine Verschiebung um drei Stellen, entspricht somit dem Schlüssel „C“.
Während das Prinzip hinter der Cäsar-Verschlüsselung relativ leicht zu durchschauen ist, beruhen moderne Chiffrierungen heute auf komplexeren mathematischen Funktionen, sogenannten Algorithmen, die mehrere Substitutionen und Transmutationen kombinieren und durch Schlüssel in Form von Passwörtern oder Binärcodes parametrisiert werden. Diese Verfahren stellen für Kryptoanalytiker (Codeknacker) deutlich größere Hürden dar. Viele etablierten Kryptosysteme gelten mit den heute zur Verfügung stehenden Mittel als unknackbar.
Wie funktioniert Verschlüsselung?
Ein Verschlüsselungsverfahren besteht grundsätzlich aus zwei Komponenten: einem kryptografischen Algorithmus und mindestens einem geheimen Schlüssel. Während der Algorithmus die Verschlüsselungsmethode beschreibt (z. B. „Verschiebe jeden Buchstaben entlang der Reihenfolge des Alphabets“), liefert der Schlüssel die Parameter (z. B. „C = drei Schritte“). Eine Verschlüsselung lässt sich somit als Verfahren beschreiben, bei dem man einem kryptografischen Algorithmus den Klartext und einen Schlüssel übergibt und einen Geheimtext als Ausgabe erhält.
Digitale Schlüssel
Bei modernen Chiffrierungsverfahren kommen digitale Schlüssel in Form von Bitfolgen zum Einsatz. Ein wesentliches Kriterium für die Sicherheit der Verschlüsselung ist die Schlüssellänge in Bits. Diese gibt das logarithmische Maß für die Anzahl der möglichen Schlüsselkombinationen an. Man spricht in diesem Fall auch vom Schlüsselraum. Je größer der Schlüsselraum, desto widerstandsfähiger ist eine Chiffrierung gegen sogenannte Brute-Force-Attacken – eine Lösungsmethode, die auf dem Ausprobieren aller möglichen Kombinationen beruht.
Verdeutlichen lassen sich Brute-Force-Attacken an der Cäsar-Verschlüsselung. Deren Schlüsselraum liegt bei 25 – das entspricht einer Schlüssellänge von unter 5 bit. Ein Codeknacker muss lediglich 25 Kombinationen durchprobieren, um den Klartext zu entziffern. Ein ernstzunehmendes Hindernis stellt die Cäsar-Verschlüsselung somit nicht dar. Moderne Verschlüsselungsverfahren hingegen nutzen Schlüssel, die deutlich mehr Zustände abbilden können. Der Advanced Encryption Standard (AES) beispielsweise bietet die Möglichkeit, Schlüssellängen von 128, 192 oder 256 bit zu wählen. Entsprechend groß ist der Schlüsselraum dieses Verfahrens.
Bereits mit einer 128-bit-Verschlüsselung lassen sich 2128 Zustände abbilden. Dies entspricht mehr als 340 Sextillionen möglichen Schlüsselkombinationen. Arbeitet AES mit 256 bit, beträgt die Anzahl der möglichen Schlüssel mehr als 115 Duodezilliarden. Selbst mit entsprechender technischer Ausrüstung würde es eine Ewigkeit dauern, alle möglichen Kombinationen auszuprobieren. Mit der heute zur Verfügung stehenden Technik sind Brute-Force-Attacken auf den AES-Schlüsselraum somit nicht praktikabel. Laut Heise würde ein Cluster aus 1 Billion PCs, von denen jedes Gerät 1 Billion Schlüssel pro Sekunde ausprobiert, immer noch 10 Millionen Jahre rechnen müssen, um eine 128-bit-Verschlüsselung zu knacken.
Das Kerckhoffs’sche Prinzip
Aufgrund der gängigen Schlüssellängen stellen Brute-Force-Attacken für moderne Verschlüsselungsverfahren keine erstzunehmende Bedrohung mehr dar. Stattdessen suchen Codeknacker Schwächen im Algorithmus, die es ermöglichen, die Rechenzeit für das Entziffern verschlüsselter Daten zu reduzieren. Eine andere Herangehensweise konzentriert sich auf sogenannte Seitenkanalangriffe, die die Implementierung eines Kryptosystems in einem Gerät oder einer Software ins Visier nehmen. Die Geheimhaltung eines Verschlüsselungsverfahrens ist dabei eher kontraproduktiv für dessen Sicherheit.
Dem Kerckhoffs’schen Prinzip zufolge beruht die Sicherheit eines Kryptosystems nicht auf der Geheimhaltung des Algorithmus, sondern auf der des Schlüssels. Bereits im Jahr 1883 formulierte Auguste Kerckhoffs einen der Grundsätze der modernen Kryptografie: Um einen Klartext zuverlässig zu verschlüsseln, genügt es, ein bekanntes, gut beschriebenes mathematisches Verfahren mit geheimen Parametern zu versehen. An dieser Annahme hat sich bis heute im Wesentlichen nichts geändert.
Wie vielen anderen Bereichen des Software-Engineerings liegt auch der Entwicklung von Verschlüsselungsmechanismen die Annahme zugrunde, dass Open Source nicht zu Lasten der Sicherheit geht. Vielmehr führt eine konsequente Anwendung des Kerckhoffs’schen Prinzips dazu, dass Fehler in kryptografischen Algorithmen schneller entdeckt werden, da entsprechende Verfahren den kritischen Augen der Fachwelt standhalten müssen.
Schlüsselexpansion: Vom Passwort zum Schlüssel
Endnutzer, die Daten chiffrieren oder dechiffrieren möchten, kommen in der Regel nicht mit Schlüsseln in Berührung, sondern nutzen eine handlichere Zeichenfolge: das Passwort. Sichere Passwörter haben 8 bis 12 Zeichen, stellen eine Kombination aus Ziffern, Buchstaben und Sonderzeichen dar und haben gegenüber Bitfolgen einen entscheidenden Vorteil: Auch Menschen können sich Passwörter ohne größeren Aufwand merken.
Als Schlüssel sind Passwörter im Rahmen der Chiffrierung aufgrund ihrer geringen Länge jedoch ungeeignet. Viele Verschlüsselungsverfahren beinhalten daher einen Zwischenschritt, in dem ein Passwort beliebiger Länge in eine feste, dem Kryptosystem entsprechende Bitfolge umgerechnet wird. Alternativ gibt es Verfahren, bei denen die Schlüssel im Rahmen der technischen Möglichkeiten zufällig generiert werden.
Eine gängige Methode, Schlüssel aus Passwörtern zu berechnen, stellt PBKDF2 (Password-Based Key Derivation Function 2) dar. Im Rahmen dieses Verfahrens werden Passwörter um eine pseudozufällige Zeichenfolge, den sogenannten Saltwert, ergänzt und anschließend mittels kryptografischer Hashfunktionen auf Bitfolgen der gewünschten Länge abgebildet.
Bei Hashfunktionen handelt es sich um kollisionssichere Einwegfunktionen – Berechnungen, die vergleichsweise leicht durchzuführen, aber nur mit erheblichem Aufwand umzukehren sind. Als sicher bezeichnet man in der Kryptografie ein Verfahren, wenn unterschiedlichen Dokumenten unterschiedliche Hashes zugewiesen werden. Passwörter, die mittels Einwegfunktionen in Schlüssel umgerechnet wurden, lassen sich wenn überhaupt nur mit erheblichem Rechenaufwand rekonstruieren. Dies ist vergleichbar mit einer Suche im Telefonbuch: Während es ein Leichtes ist, für einen gegebenen Namen die passende Telefonnummer herauszusuchen, kann die Suche nach einem Namen anhand der Telefonnummer zum unlösbaren Problem werden.
Die mathematische Berechnung wird im Rahmen von PBKDF2 in mehreren Iterationen (Wiederholungen) durchgeführt, um den auf diese Art generierten Schlüssel gegen Brute-Force-Angriffe zu schützen. Der Saltwert erhöht den Aufwand bei der Rekonstruktion eines Passworts auf Basis von Regenbogentabellen. Dabei handelt es sich um ein Angriffsmuster, bei dem Codeknacker ausgehend von gespeicherten Hashwerten auf ein unbekanntes Passwort schließen.
Weitere Passwort-Hashing-Verfahren sind scrypt, bcrypt und LM-Hash. Letzteres gilt allerdings als veraltet und unsicher.
Das Schlüsselverteilungsproblem
Ein zentrales Problem der Kryptologie ist die Frage, wie Informationen an einem Ort verschlüsselt und an einem anderen Ort entschlüsselt werden können. Bereits Julius Cäsar war mit dem sogenannten Schlüsselverteilungsproblem konfrontiert. Wollte der Feldherr eine verschlüsselte Nachricht von Rom an die germanische Front schicken, musste er sicherstellen, dass der Empfänger in der Lage war, die Geheimbotschaft zu dechiffrieren. Die einzige Lösung: Nicht nur der Geheimtext, auch der Schlüssel musste durch einen Boten übermittelt werden. Doch wie gelingt die Übergabe des Schüssels ohne Gefahr, dass dieser Dritten in die Hände fällt?
Die gleiche Frage beschäftigt Kryptologen bei der Übertragung verschlüsselter Daten im Internet noch heute. Lösungsvorschläge sind in die Entwicklung diverser Kryptosysteme und Schlüsselaustauschprotokolle eingeflossen. Das Schlüsselverteilungsproblem symmetrischer Kryptosysteme kann als Hauptmotivation für die Entwicklung asymmetrischer Verschlüsselungsverfahren betrachtet werden.
Zur Klassifikation von Verschlüsselungsverfahren
In der modernen Kryptologie unterscheidet man grundsätzlich zwischen symmetrischen und asymmetrischen Verschlüsselungsverfahren. Die Klassifikation erfolgt anhand der Schlüsselhandhabung.
Bei symmetrischen Kryptosystemen kommt ein und derselbe Schlüssel sowohl zur Chiffrierung als auch zur Dechiffrierung verschlüsselter Daten zum Einsatz. Möchten zwei kommunizierende Parteien chiffrierte Daten austauschen, muss ein Weg gefunden werden, auch den gemeinsamen Schlüssel geheim zu übermitteln. Bei asymmetrischen Kryptosystemen hingegen erzeugt jeder Kommunikationspartner ein eigenes Schlüsselpaar: einen öffentlichen Schlüssel (Public Key) und einen privaten Schlüssel (Private Key).
Kommen symmetrische und asymmetrische Verschlüsselungsverfahren in Kombination zum Einsatz, spricht man von Hybridverfahren.
Symmetrische Verschlüsselungsverfahren
Bis in die 1970er Jahre basierte die Verschlüsselung von Informationen auf symmetrischen Kryptosystemen, deren Ursprünge in antiken Verfahren wie der Cäsar-Verschlüsselung liegen. Das Grundprinzip symmetrischer Verschlüsselung ist, dass Chiffrierung und Dechiffrierung mithilfe ein und desselben Schlüssels erfolgen. Möchten zwei Parteien verschlüsselt kommunizieren, muss sowohl der Sender als auch der Empfänger über eine Kopie des gemeinsamen Schlüssels verfügen. Um chiffrierte Informationen vor dem Zugriff Dritter zu schützen, wird der symmetrische Schlüssel geheim gehalten. Man spricht daher auch von einem Private-Key-Verfahren.
Während klassische symmetrische Verschlüsselungsverfahren auf Buchstabenebene arbeiten, um Klartexte in Geheimtexte umzuschreiben, erfolgt die Chiffrierung bei computergestützten Kryptosystemen auf Bit-Ebene. Man unterscheidet dabei zwischen Stromverschlüsselungen und Blockverschlüsselungen.
- Stromverschlüsselung: Jedes Zeichen bzw. Bit des Klartextes wird mit einem Zeichen bzw. Bit des Schlüsselstroms verknüpft und somit in ein chiffriertes Ausgabezeichen übersetzt.
- Blockverschlüsselung: Die zu verschlüsselnden Zeichen bzw. Bits werden in Blöcke fester Länge zusammengefasst und auf ein Chiffrat fester Länge abgebildet.
Gängige Verschlüsselungsmethoden symmetrischer Kryptosysteme sind vergleichsweise einfache Operationen wie Substitutionen und Transpositionen, die bei modernen Verfahren kombiniert und in mehreren aufeinanderfolgenden Runden (Iterationen) auf den Klartext angewendet werden. Zudem fließen Additionen, Multiplikationen, Modulare Arithmetik und XOR-Operationen in moderne symmetrische Verschlüsselungsalgorithmen ein.
Bekannte symmetrische Verschlüsselungsverfahren sind der inzwischen überholte Data Encryption Standard (DES) und dessen Nachfolger Advanced Encryption Standard (AES).
Data Encryption Standard (DES)
Bei DES handelt es sich um ein symmetrisches Verschlüsselungsverfahren, das in den 1970er Jahren von IBM entwickelt und 1977 durch das US-amerikanische National Institute of Standards and Technology (NIST) standardisiert wurde. Als erstes nach damaligen Maßstäben ausreichend sicheres, computergestütztes Verschlüsselungsverfahren begründet DES die Anfänge der modernen Kryptografie. Der Standard ist frei von Patentrechten, gilt aufgrund der geringen Schlüssellänge von 64 bit (effektiv nur 56 bit) heute jedoch als veraltet. Bereits 1994 wurde das Kryptosystem mit zwölf HP-9735-Workstations und einem Rechenaufwand von 50 Tagen geknackt. Mit dem heutigen Stand der Technik lässt sich ein DES-Schlüssel durch Brute-Force-Angriffe bereits in wenigen Stunden entziffern.
Der symmetrische Algorithmus arbeitet als Blockverschlüsselung auf Bit-Ebene. Dabei wird der Klartext in Blöcke von 64 bit zerlegt, die einzeln mit einem 64-bit-Schlüssel chiffriert werden. Es werden somit jeweils 64 bit Klartext in 64 bit Geheimtext übersetzt. Da jedes achte Bit des Schlüssels als Paritäts-Bit fungiert, stehen für die Verschlüsselung effektiv nur 56 bit zur Verfügung.
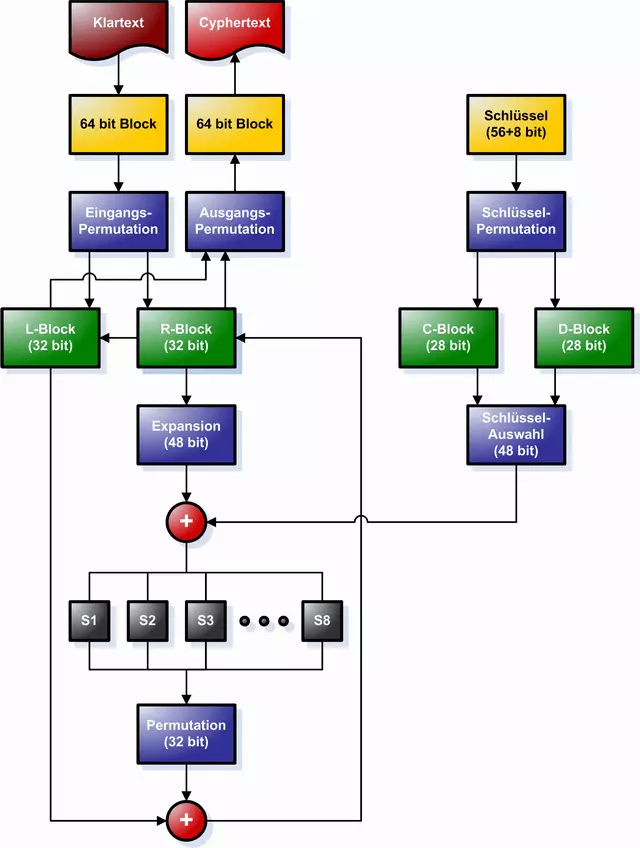
Der DES-Verschlüsselungsalgorithmus stellt ein sogenanntes Feistelnetzwerk dar und beruht auf einer Kombination von Substitutionen und Transpositionen, die in 16 Iterationen durchgeführt werden. Das nach dem IBM-Mitarbeiter Horst Feistel benannte Verfahren lässt sich in vier Schritten beschreiben:
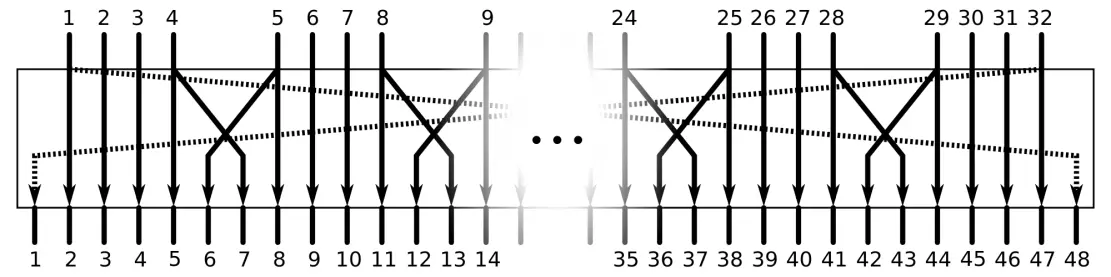
1. Eingangspermutation: Der 64 bit umfassende Klartext-Block wird einer Eingangspermutation unterzogen, die die Reihenfolge der Bits verändert. Das Ergebnis dieser Permutation wird in zwei 32-bit-Register geschrieben. Es entsteht eine linke Blockhälfte (L) und eine rechte Blockhälfte (R).
2. Schlüsselpermutation: Die für die Chiffrierung relevanten 56 bit des Schlüssels werden ebenfalls einer Permutation unterzogen und anschließend in zwei 28 bit große Blöcke aufgeteilt (C und D). Für jede der 16 Iterationen wird aus den beiden Schlüsselblöcken C und D ein Rundenschlüssel generiert. Dazu werden die Bits beider Halbblöcke um jeweils 1 oder 2 bit zyklisch nach links verschoben. Dies soll sicherstellen, dass in jeder Verschlüsselungsrunde ein anderer Rundenschlüssel eingerechnet wird. Anschließend werden die beiden Halbblöcke C und D auf einen 48-bit-Rundenschlüssel abgebildet.
3. Verschlüsselungsrunden: Jede Verschlüsselungsrunde umfasst die Schritte a) bis d). Pro Schleife gehen jeweils ein Halbblock R und ein Rundenschlüssel in die Verschlüsselung ein. Der Halbblock L bleibt zunächst außen vor.
- Expansion: Der Halbblock R wird mittels Expansion auf einen 48-bit-Block erweitert. Dazu werden die 32 bit des Halbblocks im Rahmen der Expansion in 4-bit-Gruppen aufgeteilt und entsprechend folgendem Schema teilweise dupliziert und permutiert:
- XOR-Verknüpfung von Datenblock und Rundenschlüssel: In jeder Verschlüsselungsrunde wird der auf 48 bit expandierte Block R mit einem 48-bit-Rundenschlüssel mittels einer XOR-Operation verknüpft. Das Ergebnis der XOR-Verknüpfung ist wiederum ein 48-bit-Block.
- S-Boxen (Substitutionsboxen): Im Anschluss an die XOR-Verknüpfung wird der 48-bit-Block in acht 6-bit-Blöcke aufgeteilt, mithilfe von S-Boxen durch acht 4-bit-Blöcke substituiert und zu einem 32-bit-Block zusammengefasst. Das Ergebnis der Substitutionsboxen wird erneut einer Permutation unterzogen.
- XOR-Verknüpfung von R-Block und L-Block: Nach jeder Verschlüsselungsrunde wird das Ergebnis der S-Boxen mittels XOR mit dem bisher ungenutzten L-Block verknüpft. Das Ergebnis ist ein 32-bit-Block, der als neuer R-Block in die zweite Verschlüsselungsrunde eingeht. Der R-Block der ersten Runde dient als L-Block der zweiten Runde.
2. Ausgangspermutation: Wurden alle 16 Verschlüsselungsrunden durchlaufen, werden L- und R-Block zu einem 64-bit-Block zusammengefasst und einer zur Eingangspermutation inversen Ausgangspermutation unterzogen. Der Klartext ist nun chiffriert.
Folgende Grafik zeigt eine schematische Darstellung des DES-Algorithmus. Die XOR-Verknüpfungen sind als rote Kreise mit weißem Kreuzen gekennzeichnet.
Die Entschlüsselung eines per DES chiffrierten Geheimtextes erfolgt nach demselben Schema in umgekehrter Reihenfolge.
Ein Hauptkritikpunkt an DES ist die geringe Schlüssellänge von 56 bit, die in einem vergleichsweise kleinen Schlüsselraum resultiert. Dieser kann Brute-Force-Angriffen mit der heute zur Verfügung stehenden Rechenleistung nicht mehr standhalten. Zudem wird das Verfahren der Schlüsselpermutation, das 16 nahezu identische Rundenschlüssel erzeugt, als zu schwach eingeschätzt.
Mit Triple-DES (3DES) wurde eine Variante von DES entwickelt, bei der das Verschlüsselungsverfahren in drei aufeinanderfolgenden Runden durchlaufen wird. Doch auch die effektive Schlüssellänge von 3DES beträgt effektiv lediglich 112 bit und liegt damit noch immer unter dem heutigen Mindeststandard von 128 bit. Zudem ist 3DES deutlich rechenintensiver als DES.
Der Data Encryption Standard wurde daher weitgehend ersetzt. Als Nachfolger gilt der ebenfalls symmetrische Verschlüsselungsalgorithmus Advanced Encryption Standard.
Advanced Encryption Standard (AES)
In den 1990er Jahren zeichnete sich ab, dass der bis dato meistgenutzte Verschlüsselungsstandard DES der technischen Entwicklung nicht mehr gewachsen war. Ein neuer Verschlüsselungsstandard musste her. Als Nachfolger etablierte sich der nach seinen Entwicklern Vincent Rijmen und Joan Daemen benannte Rijndael-Algorithmus (Aussprache: „Reindahl“) – ein Verfahren, das sich aufgrund seiner Sicherheit, Flexibilität und Performance in einer öffentlichen Ausschreibung durchsetzte und Ende 2000 vom NIST als Advanced Encryption Standard (AES) zertifiziert wurde.
Auch AES teilt den zu verschlüsselnden Klartext in Blöcke auf. Somit beruht auch dieses Kryptosystem wie DES auf einer Blockverschlüsselung. Der Standard unterstützt 128-, 192- und 256-bit-Schlüssel. Statt 64-bit-Blöcken kommen bei AES jedoch deutlich größere 128-bit-Blöcke zum Einsatz, die mit Hilfe eines Substitutions-Permutations-Netzwerks (SPN) in mehreren aufeinanderfolgenden Runden chiffriert werden. Auch der DES-Nachfolger verwendet bei jeder Verschlüsselungsrunde einen neuen Rundenschlüssel, der rekursiv aus dem Ausgangsschlüssel abgeleitet und mittels XOR mit dem zu verschlüsselnden Datenblock verknüpft wird. Der Ablauf der Verschlüsselung lässt sich grob in vier Schritte unterteilen:
1. Schlüsselexpansion: Wie DES nutzt auch AES in jeder Verschlüsselungsschleife einen neuen Rundenschlüssel. Dieser wird durch Rekursion aus dem Ausgangsschlüssel abgeleitet. Dabei wird der Ausgangsschlüssel auf eine Länge expandiert, die es ermöglicht, die benötigte Anzahl an 128-bit-Rundenschlüsseln abzubilden. Jeder Rundenschlüssel basiert somit auf einem Teilabschnitt des erweiterten Ausgangsschlüssels. Die Anzahl der benötigten Rundenschlüssel beträgt die Anzahl der Verschlüsselungsrunden (R) inklusive Schlussrunde plus einen Rundenschlüssel für die Vorrunde (Anzahl der Rundenschlüssel = R + 1).
2. Vorrunde: In der Vorrunde wird der 128-bit-Eingabeblock in eine zweidimensionale Tabelle (Array) übertragen und mittels XOR mit dem ersten Rundenschlüssel verknüpft (KeyAddition). Die Tabelle umfasst 4 Zeilen und 4 Spalten. Jede Zelle enthält somit ein Byte (8 bit) des zu verschlüsselnden Blocks.
3. Verschlüsselungsrunden: Die Anzahl der Verschlüsselungsrunden hängt von der verwendeten Schlüssellänge ab: 10 Runden bei AES128, 12 Runden bei AES192 und 14 Runden bei AES256. In jeder Verschlüsselungsrunde kommen folgende Operationen zum Einsatz:
- SubBytes: Bei SubBytes handelt es sich um eine monoalphabetische Substitution. Dabei wird jedes Byte im zu verschlüsselnden Block mithilfe einer S-Box durch ein Äquivalent ersetzt.
- ShiftRows: Im Rahmen der ShiftRow-Transformation werden die Bytes in den Zellen des Arrays (siehe Vorrunde) zyklisch nach links verschoben.
- MixColumns: Mit MixColumns beinhaltet der AES-Algorithmus eine Transformation, bei der die Daten innerhalb der Spalten des Arrays vermischt werden. Dieser Schritt fußt auf einer Neuberechnung jeder einzelnen Zelle. Dazu werden die Spalten des Arrays einer Matrizenmultiplikation unterzogen und die Ergebnisse mittels XOR verknüpft.
- KeyAddition: Am Ende jeder Verschlüsselungsrunde findet eine weitere KeyAddition statt. Diese beruht wie in der Vorrunde auf einer XOR-Verknüpfung des Datenblocks mit dem aktuellen Rundenschlüssel.
4. Schlussrunde: Die Schlussrunde ist die letzte Verschlüsselungsrunde. Anders als die vorhergehenden Runden beinhaltet diese keine MixColumns-Transformationen und umfasst somit lediglich die Operationen SubBytes, ShiftRows und KeyAddition. Das Ergebnis der Schlussrunde ist der Geheimtext.
Die Entschlüsselung von AES-chiffrierten Daten beruht auf der Investierung des Verschlüsselungsalgorithmus. Diese bezieht sich neben der Abfolge der Arbeitsschritte auch auf die Operationen ShiftRow, MixColumns und SubBytes, deren Richtung ebenfalls umgekehrt wird.
AES wird aufgrund seines Algorithmus eine hohe Sicherheit bescheinigt. Bis heute ist kein praxisrelevanter Angriff bekannt. Brute-Force-Angriffe sind wegen der Schlüssellänge von mindestens 128 bit ineffizient. Zudem sorgen Operationen wie ShiftRows und MixColumns für eine optimale Durchmischung der Bits: Im Resultat ist jedes Bit vom Schlüssel abhängig. Zudem überzeugt das Kryptosystem durch eine einfache Implementierung und eine hohe Geschwindigkeit. Anwendung findet AES u. a. als Verschlüsselungsstandard bei WPA2, SSH und IPSec. Zudem wird der Algorithmus zur Verschlüsselung komprimierter Dateiarchive wie 7-Zip oder RAR verwendet.
Sicher vor dem Zugriff Dritter sind AES-chiffrierte Daten jedoch nur solange, wie der Schlüssel geheim bleibt. Da ein und derselbe Schlüssel zur Chiffrierung und Dechiffrierung verwendet wird, ist das Kryptosystem wie jedes andere symmetrische Verfahren vom Schlüsselverteilungsproblem betroffen. Der sichere Einsatz von AES beschränkt sich somit auf Anwendungsfelder, die keinen Schlüsselaustausch erfordern oder diesen über einen sicheren Kanal ermöglichen.
Die verschlüsselte Kommunikation im Internet erfordert es jedoch, dass Daten auf einem Rechner chiffriert und auf einem anderen dechiffriert werden. Hier haben sich asymmetrische Kryptosysteme durchgesetzt, die einen sicheren Austausch symmetrischer Schlüssel ermöglichen oder ohne den Austausch eines gemeinsamen Schlüssels funktionieren.
Als Alternativen zu AES bieten sich die ebenfalls auf einer Blockverschlüsselung basierenden symmetrischen Kryptosysteme MARS, RC6, Serpent und Twofish an, die neben Rijndael zu den Finalisten der AES-Ausschreibung zählten. Auch der Twofish-Vorgänger Blowfish ist nach wie vor im Einsatz. Beachtung findet zudem die Stromverschlüsselung Salsa20, die 2005 von Daniel J. Bernstein entwickelt wurde und zu den Finalisten des europäischen eSTREAM-Projekts gehört.
Asymmetrische Verschlüsselungsverfahren
Während bei symmetrischen Kryptosystemen auf beiden Seiten der chiffrierten Kommunikation der gleiche Schlüssel zum Einsatz kommt, erzeugen die beiden Parteien einer asymmetrisch verschlüsselten Kommunikation pro Seite jeweils ein Schlüsselpaar. Jeder Kommunikationsteilnehmer verfügt somit über zwei Schlüssel: einen öffentlichen und einen privaten. Um verschlüsselt kommunizieren zu können, muss jede Partei ihren öffentlichen Schlüssel bekanntgeben. Dies erfolgt in der Regel über Schlüsselserver. Man spricht von einem Public-Key-Verfahren. Der private Schlüssel hingegen bleibt geheim. Hier zeigt sich die Stärke asymmetrischer Kryptosysteme: Anders als bei symmetrischen Verschlüsselungsverfahren wird der geheime Schlüssel zu keiner Zeit aus der Hand gegeben.
Im Rahmen einer asymmetrischen Verschlüsselung dienen öffentliche Schlüssel der Chiffrierung. Zudem erlauben sie, digitale Signaturen zu prüfen und Benutzer zu verifizieren. Private Schlüssel hingegen kommen bei der Dechiffrierung zum Einsatz und ermöglichen es, digitale Signaturen zu erzeugen oder sich gegenüber anderen Benutzern zu authentifizieren.
Ein Beispiel:
Benutzer A möchte Benutzer B eine chiffrierte Nachricht senden. Dazu benötigt A den öffentlichen Schlüssel von B. Der öffentliche Schlüssel von B ermöglicht es A, eine Nachricht so zu chiffrieren, dass sie nur mit dem privaten Schlüssel von B dechiffriert werden kann. Abgesehen von B ist somit niemand in der Lage, die Nachricht zu lesen. Selbst A hat nach der Verschlüsselung keine Möglichkeit mehr, die Nachricht zu entschlüsseln.
Der Vorteil der asymmetrischen Verschlüsselung besteht somit darin, dass prinzipiell jeder den öffentlichen Schlüssel von Benutzer B verwenden kann, um Nachrichten zu chiffrieren, die aber ausschließlich B mit seinem geheimen Schlüssel dechiffrieren kann. Da lediglich der öffentliche Schlüssel ausgetauscht wird, kann man auf einen abhörsicheren, manipulationsgeschützten Kanal verzichten.
Ein Nachteil dieses Verschlüsselungsverfahrens ist jedoch, dass B sich nicht sicher sein kann, dass die chiffrierte Nachricht tatsächlich von A stammt. Denn grundsätzlich könnte auch ein Dritter (C) den öffentlichen Schlüssel von B nutzen, um Nachrichten zu verschlüsseln – beispielsweise, um Malware zu verbreiten. Zudem kann A sich nicht sicher sein, dass es sich bei einem öffentlichen Schlüssel tatsächlich um den von B handelt. Auch C könnte einen öffentlichen Schlüssel erstellen und diesen als den von B ausgeben, um Nachrichten von A zu B abzufangen. Im Rahmen der asymmetrischen Verschlüsselung wird somit ein Mechanismus benötigt, mit dem ein Kommunikationspartner die Authentizität des anderen prüfen kann.
Lösen lässt sich dieses Problem durch digitale Zertifikate und Signaturen.
- Digitale Zertifikate: Um asymmetrische Verschlüsselungsverfahren sicher zu gestalten, haben Kommunikationspartner die Möglichkeit, die Echtheit ihrer öffentlichen Schlüssel durch eine offizielle Zertifizierungsstelle bestätigen zu lassen. Ein gängiger Standard für Public-Key-Zertifikate ist X.509. Anwendung findet dieser beispielsweise bei der TLS/SSL-verschlüsselten Datenübertragung via HTTPS oder im Rahmen der E-Mail-Verschlüsselung via S/MIME.
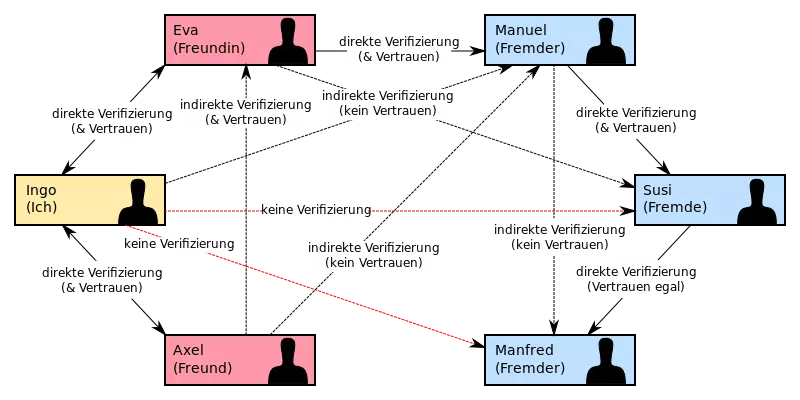
- Digitale Signaturen: Während digitale Zertifikate verwendet werden, um öffentliche Schlüssel zu verifizieren, kommen digitale Signaturen zum Einsatz, um den Absender einer verschlüsselten Nachricht zweifelsfrei zu identifizieren.Dazu nutzt dieser seinen privaten Schlüssel, um eine Signatur zu erzeugen. Anschließend verifiziert der Empfänger diese Signatur mithilfe des öffentlichen Schlüssels des Absenders. Die Echtheit digitaler Signaturen lässt sich durch hierarchisch strukturierte Public-Key-Infrastrukturen (PKI) sicherstellen. Ein Beispiel dafür ist das DE-Mail-System. Eine dezentrale Alternative zur hierarchischen PKI ist das sogenannte Web of Trust (WOT), ein Netzwerk, in dem sich Nutzer gegenseitig direkt und indirekt verifizieren. Folgende Grafik zeigt eine schematische Darstellung eines solchen Vertrauensnetzwerks:
Die erste wissenschaftliche Veröffentlichung eines asymmetrischen Verschlüsselungsverfahrens erfolgte 1977 durch die Mathematiker Rivest, Shamir und Adleman. Das nach den Erfindern benannte RSA-Verfahren basiert auf Einwegfunktionen mit Falltür und lässt sich zur Verschlüsselung von Daten sowie als Signaturverfahren einsetzen.
Rivest, Shamir, Adleman (RSA)
RSA gilt als eines der sichersten und bestbeschriebenen Public-Key-Verfahren. Die Idee, eine Verschlüsselung durch einen öffentlichen Chiffrierschlüssel und einen geheimen Dechiffrierschlüssel zu realisieren, geht auf die Kryptologen Whitfield Diffie und Martin Hellman zurück. Diese veröffentlichten 1976 mit dem Diffie-Hellman-Schlüsselaustausch ein Verfahren, das es zwei Kommunikationspartnern ermöglicht, sich über einen unsicheren Kanal gemeinsam auf einen geheimen Schlüssel zu einigen. Dabei stützten sich die Forscher auf das von Ralph Merkle entwickelte Merkles Puzzle. Man spricht daher auch vom Diffie-Hellman-Merkle-Schlüsselaustausch (DHM).
Die Kryptogen bedienten sich mathematischer Einwegfunktionen, die zwar leicht durchzuführen sind, sich aber nur mit erheblichem Rechenaufwand umkehren lassen. Noch heute kommt der nach ihnen benannte Schlüsselaustausch zur Anwendung, um geheime Schlüssel im Rahmen symmetrischer Kryptosysteme auszuhandeln. Ein weiteres Verdienst des Forscherduos stellt das Konzept der Falltür dar. Bereits in der Veröffentlichung des Diffie-Hellman-Schlüsselaustauschs werden versteckte Abkürzungen angesprochen, die es ermöglichen sollen, die Inversion einer Einwegfunktion zu beschleunigen. Einen konkreten Beweis lieferten Diffie und Hellmann nicht, regten mit ihrer Theorie der Falltür jedoch zahlreiche Kryptologen zu eigenen Untersuchungen an.
Auch Rivest, Shamir und Adleman suchten nach Abkürzungen für Einwegfunktionen – ursprünglich mit der Motivation, die Falltürtheorie zu widerlegen. Doch ihre Forschung entwickelte sich in eine andere Richtung und mündete in das schließlich nach ihnen benannte Verschlüsselungsverfahren. Heute gilt RSA als der erste wissenschaftlich publizierte Algorithmus, der eine Übertragung chiffrierter Daten ohne Austausch eines geheimen Schlüssels ermöglicht.
Beim RSA kommt ein Algorithmus zum Einsatz, der sich auf die Multiplikation großer Primzahlen stützt. Während es im Allgemeinen kein Problem darstellt, zwei Primzahlen mit 100, 200 oder 300 Stellen zu multiplizieren, existiert bis heute kein effizienter Algorithmus, der das Ergebnis einer solchen Rechenoperation im Umkehrschritt in ihre Primfaktoren zerlegen kann. Verdeutlichen lässt sich die Primfaktorisierung an einem Beispiel:
Multipliziert man die Primzahlen 14.629 und 30.491 erhält man das Produkt 446.052.839. Dieses hat lediglich vier Teiler: 1, sich selbst sowie die beiden Primzahlen, die multipliziert wurden. Streicht man die ersten beiden Teiler, da jede Zahl durch 1 und durch sich selbst teilbar ist, erhält man somit die Ausgangswerte 14.629 und 30.491.
Dieses Schema ist die Grundlage der RSA-Schlüsselerzeugung. Sowohl der öffentliche als auch der private Schlüssel stellen zwei Zahlenpaare dar:
Öffentlicher Schlüssel: (e, N)
Privater Schlüssel: (d, N)
Bei N handelt es sich um das sogenannte RSA-Modul. Dieses ist in beiden Schlüsseln enthalten und ergibt sich aus dem Produkt zweier zufällig gewählter, sehr großer Primzahlen p und q (N = p x q).
Um den öffentlichen Schlüssel zu generieren, benötigt man zudem e, eine Zahl, die mit gewissen Einschränkungen zufällig gewählt wird. Kombiniert man N und e erhält man den öffentlichen Schlüssel, der jedem Kommunikationsteilnehmer in Klartext vorliegt.
Um den private Schlüssel zu generieren, benötigt neben N auch d. Bei d handelt es sich um einen Wert, der sich aus den zufällig generierten Primzahlen p und q sowie der Zufallszahl e ergibt, die auf Basis der Eulerschen Phi-Funktion (φ) miteinander verrechnet werden.
Welche Primzahlen in die Berechnung des privaten Schlüssels eingehen, muss geheim bleiben, um die Sicherheit der RSA-Verschlüsselung zu gewährleisten. Das Produkt der beiden Primzahlen hingegen kann im öffentlichen Schlüssel in Klartext verwendet werden, da man davon ausgeht, dass es heutzutage keinen effizienten Algorithmus gibt, der das Produkt sehr großer Primzahlen in relevanter Zeit in seine Faktoren zerlegen kann. Es ist somit nicht möglich, p und q aus N zu berechnen. Es sei denn, man kann die Berechnung abkürzen. Eine solche Falltür stellt der Wert d dar, der lediglich dem Besitzer des privaten Schlüssels bekannt ist.
Die Sicherheit des RSA-Algorithmus ist in hohem Maße abhängig vom technischen Fortschritt. Die Rechenleistung von Computern verdoppelt sich in etwa alle zwei Jahre. Es ist somit nicht ausgeschlossen, dass in absehbarer Zeit ein effizientes Verfahren zur Primfaktorzerlegung in der heute üblichen Größenordnung zur Verfügung steht. In diesem Fall bietet RSA die Möglichkeit, den Algorithmus der technischen Entwicklung anzupassen, indem zur Berechnung der Schlüssel noch größere Primzahlen herangezogen werden.
Für einen sicheren Betrieb des RSA-Verfahrens gibt die Bundesnetzagentur für den Wert N (das Produkt beider Primzahlen) bis Ende 2020 eine Mindestlänge von 1.976 bit an, empfiehlt jedoch 2.048 bit. Dies entspricht Primzahlen in einer Größenordnung von etwa 300 Dezimalstellen.
ID-basierte Public-Key-Verfahren
Die zentrale Schwachstelle asymmetrischer Verschlüsselungssysteme ist die Benutzerauthentifizierung. In klassischen Public-Key-Verfahren steht ein öffentlicher Schlüssel in keinerlei Zusammenhang mit der Identität seines Benutzers. Gelingt es einem Dritten, sich mithilfe seines eigenen Public Keys als eine der an der verschlüsselten Datenübertragung beteiligten Parteien auszugeben, lässt sich das gesamte Kryptosystem aushebeln, ohne dass der Algorithmus oder ein privater Dechiffrierschlüssel direkt angegriffen werden müssen. Bereits 1984 schlug Adi Shamir, Mitentwickler der RSA, daher ein ID-basiertes Kryptosystem vor, das auf dem asymmetrischen Ansatz basiert, dessen Schwachstelle jedoch zu kompensieren versucht.
Im Rahmen der identitätsbasierten Verschlüsselung („identity-based encryption“, IBE) wird der Public Key eines Kommunikationspartners nicht in Abhängigkeit zum Private Key erzeugt, sondern aus einer eindeutigen ID berechnet. Je nach Kontext bieten sich beispielsweise die E-Mail-Adresse oder eine Domain an. Es entfällt somit die Authentifizierung öffentlicher Schlüssel durch offizielle Zertifizierungsstellen. Deren Platz nimmt jedoch eine andere Instanz ein: der sogenannte Private Key Generator (PKG). Dabei handelt es sich um einen zentralen Algorithmus, bei dem sich der Empfänger einer verschlüsselten Nachricht einen zu seiner Identität gehörigen Dechiffrierschlüssel ausstellen lassen kann.
Die Theorie der ID-basierten Verschlüsselung löst somit ein grundlegendes Problem asymmetrischer Kryptosysteme, führt jedoch zwei weitere Sicherheitslücken ein: Ein zentraler Kritikpunkt ergibt sich aus der Frage, wie die Übergabe des privaten Dechiffrierschlüssels vom PKG zum Empfänger der verschlüsselten Nachricht erfolgen soll. Hier tut sich das altbekannte Schlüsselverteilungsproblem auf. Einen weiteren Nachteil ID-basierter Verfahren stellt der Umstand dar, dass es mit dem PKG neben dem Empfänger einer chiffrierten Nachricht eine weitere Instanz gibt, die den Dechiffrierschlüssel kennt. Dieser ist somit per Definition kein Private Key und kann missbräuchlich eingesetzt werden. Theoretisch hat der PKG die Möglichkeit, sämtliche Nachrichten unautorisiert zu entschlüsseln. Umgehen lässt sich dies, indem das Schlüsselpaar mit Open-Source-Software auf dem eigenen Rechner generiert wird.
Das bekannteste ID-basierte Verfahren geht auf Dan Boneh und Matthew K. Franklin zurück.
Hybrid-Verfahren
Als Hybrid-Verschlüsselung bezeichnet man die Verbindung symmetrischer und asymmetrischer Kryptosysteme im Rahmen der Datenübertragung im Internet. Ziel dieser Kombination ist es, die Schwächen des einen Systems durch die Stärken des anderen zu kompensieren.
Symmetrische Kryptosysteme wie AES (Advanced Encryption Standard) gelten zum heutigen Stand der Technik als sicher und ermöglichen es, auch große Datenmengen schnell und recheneffizient zu verarbeiten. Das Design des Algorithmus auf Basis eines gemeinsamen Private Keys, der abhörsicher zwischen Empfänger und Sender einer chiffrierten Nachricht ausgetauscht werden muss, stellt Anwender symmetrischer Verfahren jedoch vor das Problem der Schlüsselverteilung. Lösen lässt sich dieses durch asymmetrische Kryptosysteme. Verfahren wie RSA beruhen auf einer strikten Trennung von öffentlichen und privaten Schlüsseln und ermöglichen es so, die Übergabe eines privaten Schlüssels zu umgehen.
Einen verlässlichen Schutz gegen Kryptoanalysen bietet RSA jedoch nur bei einer ausreichend großen Schlüssellänge von mindestens 1.976 bit. Diese resultiert in langen Rechenvorgängen, die den Algorithmus für eine Ver- und Entschlüsselung großer Datenmengen disqualifiziert. Zudem ist der zu übermittelnde Geheimtext nach einer RSA-Chiffrierung deutlich größer als der ursprüngliche Klartext.
Im Rahmen hybrider Verschlüsselungsverfahren kommen asymmetrische Algorithmen daher nicht zum Einsatz, um Nutzdaten zu verschlüsseln, sondern um die Übertragung eines symmetrischen Session-Keys über einen ungeschützten öffentlichen Kanal abzusichern. Dieser wiederum ermöglicht es, einen mithilfe symmetrischer Algorithmen effizient chiffrierten Geheimtext zu entschlüsseln.
Der Ablauf einer hybriden Verschlüsselung lässt sich in drei Schritten beschreiben:
1. Schlüsselverwaltung: Bei Hybrid-Verfahren wird die symmetrische Verschlüsselung einer Nachricht von einem asymmetrischen Verschlüsselungsverfahren eingerahmt. Dazu müssen sowohl asymmetrische (a) als auch symmetrische Schlüssel (b) generiert werden:
- Bevor es zur chiffrierten Datenübertragung kommt, erzeugen beide Kommunikationspartner zunächst je ein asymmetrisches Schlüsselpaar: einen Public Key und einen Private Key. Anschließend erfolgt der Austausch der öffentlichen Schlüssel – im besten Fall abgesichert durch einen Authentifizierungsmechanismus. Das asymmetrische Schlüsselpaar dient der Chiffrierung und Dechiffrierung eines symmetrischen Session-Keys und wird in der Regel mehrmals benutzt.
- Die Chiffrierung und Dechiffrierung des Klartextes erfolgt anhand des symmetrischen Sitzungsschlüssels (Session-Key). Dieser wird vom Absender einer Nachricht bei jedem Verschlüsselungsvorgang neu generiert.
2. Verschlüsselung: Soll eine (umfangreiche) Nachricht sicher über das Internet übermittelt werden, erzeugt der Absender zunächst einen symmetrischen Session-Key, mit dem die Nutzdaten chiffriert werden. Ist dies erfolgt, kommt der Public Key des Empfängers zum Einsatz. Dieser dient der asymmetrischen Chiffrierung des Sitzungsschlüssels. Sowohl die Nutzdaten als auch der symmetrische Schlüssel liegen somit in chiffrierter Form vor und können ohne Bedenken versendet werden.
3. Entschlüsselung: Geht ein Geheimtext zusammen mit dem chiffrierten Session-Key beim Empfänger ein, nutzt dieser seinen Private Key um den Sitzungsschlüssel asymmetrisch zu dechiffrieren. Dieser kommt im Anschluss zum Einsatz, um die symmetrisch chiffrierten Nutzdaten zu entschlüsseln.
Nach diesem Schema lässt sich ein effizientes Verschlüsselungsverfahren realisieren, mit dem sich selbst umfangreiche Nutzdaten in hoher Geschwindigkeit sicher ver- und entschlüsselt werden können. Da lediglich ein kurzer Sitzungsschlüssel asymmetrisch chiffriert wird, fallen die vergleichsweise langen Berechnungszeiten asymmetrischer Algorithmen bei der Hybrid-Verschlüsselung nicht ins Gewicht. Das Schlüsselverteilungsproblem des symmetrischen Verschlüsselungsverfahrens reduziert sich durch die asymmetrische Chiffrierung des Session-Keys auf das Problem der Benutzerauthentifizierung. Dieses lässt sich wie bei rein asymmetrischen Kryptosystemen durch digitale Signaturen und Zertifikate lösen.
Hybride Verschlüsselungsverfahren kommen in Form von IPSec bei der gesicherten Kommunikation über ungesicherte IP-Netze zum Einsatz. Und auch das Hypertext Transfer Protocol Secure (HTTPS) setzt mit TLS/SSL auf ein hybrides Verschlüsselungsprotokoll, das symmetrische und asymmetrische Kryptosysteme kombiniert. Zudem ist eine Umsetzung des Hybridverfahrens die Basis für Verschlüsselungsstandards wie Pretty Good Privacy (PGP), GnuPG und S/MIME, die im Rahmen der E-Mail-Verschlüsselung zum Einsatz kommen.
Eine gängige Kombination im Rahmen hybrider Verschlüsselungsverfahren ist die symmetrische Verschlüsselung der Nutzdaten via AES und die anschließende asymmetrische Verschlüsselung des Session-Key mittels RSA. Alternativ lässt sich der Session-Key im Rahmen des Diffie-Hellman-Verfahrens aushandeln. Dieses kann als Ephemeral Diffie-Hellman Forward Secrecy bieten, ist jedoch anfällig für Man-in-the-Middle-Angriffe. Einen Ersatz für den RSA-Algorithmus stellt das Elgamal-Kryptosystem dar. Das 1985 vom Taher Elgamal entwickelte Public-Key-Verfahren basiert ebenfalls auf der Idee des Diffie-Hellman-Schlüsselaustauschs und kommt in der aktuellen Version des Verschlüsselungsprogramms PGP zum Einsatz.