Median berechnen mit Excel - so geht's
Mit der Excel-Median-Funktion berechnen Sie die mittlere Zahl (Median) in einer vorhandenen Zahlengruppe. Der Median gibt Ihnen im Gegensatz zum Mittelwert nicht einen Durchschnitt, sondern die zentrale Tendenz einer nach Größe geordneten Zahlenreihe.
- Bewährt: Vollständiges Office-Paket
- Sicher: 1 TB zentraler Speicherplatz
- Ortsunabhängig: Auf bis zu 5 Geräten installierbar
Was ist der Median?
Der Median ist in der Statistik ein als Quantil bezeichneter besonderer Schwellenwert, der eine vorgegebene Reihe von Zahlen in zwei Hälften teilt. Die Zahlen bzw. Werte werden dabei nach aufsteigender Größe gemessen. Der ermittelte Median zeigt den numerischen Wert in mittlerer Position der untersuchten Zahlenreihe an.
Excel-Median-Funktion: Die Syntax erklärt
Der Median ist als Excel-Funktion besonders praktisch, um konkrete Zentralwerte zu erhalten. Um in Excel den Median zu bestimmen, nutzen Sie in den Versionen ab Office 2016 sowie in Microsoft 365 folgende Formelsyntax:
=MEDIAN(Zahl1;Zahl2;…)Die Formelsyntax der Excel-Median-Funktion besteht aus der notwendigen, numerischen Variable „Zahl1“ und optionalen, darauffolgenden Variablen, die angeben, aus welcher Zahlenreihe die Mitte zu berechnen ist. Bei den Variablen „Zahl1“, „Zahl2“ usw. kann es sich sowohl um Zahlen als auch um Zellenreferenzen handeln.
So wenden Sie die Median-Funktion an
Wenn Sie den Median einer Zahlengruppe in Excel einfügen möchten, führen Sie einen Doppelklick in einer Zelle durch und geben beispielsweise =MEDIAN(A1:E1) ein. Sie erhalten somit die Mittelzahl der numerischen Werte in den Zellen A1 bis E1. Sie können alternativ in einer tabellarischen Übersicht die Median-Formel als Spalte bzw. in eine Zeile direkt integrieren.
Beispiel:
- Wenn Sie in einer ungeraden Anzahl von Werten in den Zellen A3 bis A7 den Median suchen, geben Sie
=MEDIAN(A3:A7)ein. Sie erhalten somit den Median 3. - Wenn Sie in einer geraden Anzahl von Werten in A3 bis A8 den Median suchen, geben Sie
=MEDIAN(A3:A8)ein. Sie erhalten in dem Fall den Median 3,5, also den Wert zwischen den Zahlen an dritter und vierter Stelle.
Das ist bei Excel Median zu beachten
Die Median-Funktion ist in der Lage, den Mittelwert von 1 bis 255 (maximale Spaltenbreite in Excel) zu berechnen. Achten Sie jedoch darauf, dass es sich bei den Argumenten um numerische Werte, also ordinal skalierte Variablen, handelt. Text, Namen, Matrizen, Bezüge und logische Werte, die keine Zahlen enthalten, ignoriert die Funktion. Den Median von Wahrheitswerten und ausformulierten Zahlen wiederum kann die Funktion ermitteln.
Unterschied zu Mittel- und Modalwert
Der Median gibt die zentrale Tendenz von aufsteigenden Zahlenwerten in ihrer statistischen Aufteilung wieder. Um eine zentrale Tendenz zu ermitteln, lassen sich insgesamt drei mögliche Werte nutzen:
- Median: Gibt in einer hierarchisch geordneten Gruppe von Werten den mittleren Wert (Mittelzahl) an.
- Mittelwert: Gibt den arithmetischen Mittelwert an, indem die Summe der gegebenen Zahlen durch die Anzahl der Zahlen dividiert wird.
- Modalwert: Zeigt die am häufigsten vertretene Zahl in einer numerischen Gruppe an.
Sind Listenwerte gleichmäßig verteilt, so kann der Median dem Mittelwert bzw. dem Modalwert ähneln. Sind die Werte ungleichmäßig verteilt, so weicht der Median meist von Mittel- und Modalwert ab.
Gerade und ungerade Anzahl von Werten
Bei der Anzahl der bereitgestellten Zahlen ist zwischen einer geraden und ungeraden Anzahl von Zahlen zu unterscheiden:
- Ist die Anzahl der Werte in einer Liste ungerade, gibt der Median die Zahl in der mittleren Position der Gruppe an.
- Ist die Anzahl der Wert einer Liste gerade, bildet der Median den Durchschnitt (arithmetisches Mittel) der beiden Zahlen in der Mitte einer Zahlengruppe (Unter- und Obermedian genannt).
Median in Excel berechnen
Der Median kommt dann zur Anwendung, wenn der Zentralwert von Daten mit Ordinal-, Intervall- oder Verhältnisskalierung zu berechnen ist. Häufige Einsatzbereiche sind:
- In der deskriptiven Statistik zur Ermittlung des Zentralwerts in Stichproben
- Zur Ermittlung von mittleren Positionen in Wahrscheinlichkeitsverteilungen und Zufallsgrößen in der Wahrscheinlichkeitstheorie
- Als Maßeinheit robuster Schätzverfahren bei unbekannten Wertverteilungen in der mathematischen Statistik
Die Excel-Median-Funktion an zwei praktischen Beispielen erklärt
Um den praktischen Nutzen der Median-Funktion zu verstehen, betrachten Sie die folgenden praktischen Anwendungsbeispiele:
Beispiel 1: Median bei Einkommensermittlung
Es soll der Zentralwert von Jahreseinkommen unter eine Gruppe von acht Personen ermittelt werden. Je nach Verteilung der Einkommensgrößen kann der Mittelwert zwar das durchschnittliche Einkommen ermitteln, jedoch kein realistisches Bild wiedergeben, wenn 80 Prozent unter einem bestimmten Schwellenwert verdienen und 20 Prozent darüber. Hier kommt der Mittelwert ins Spiel.
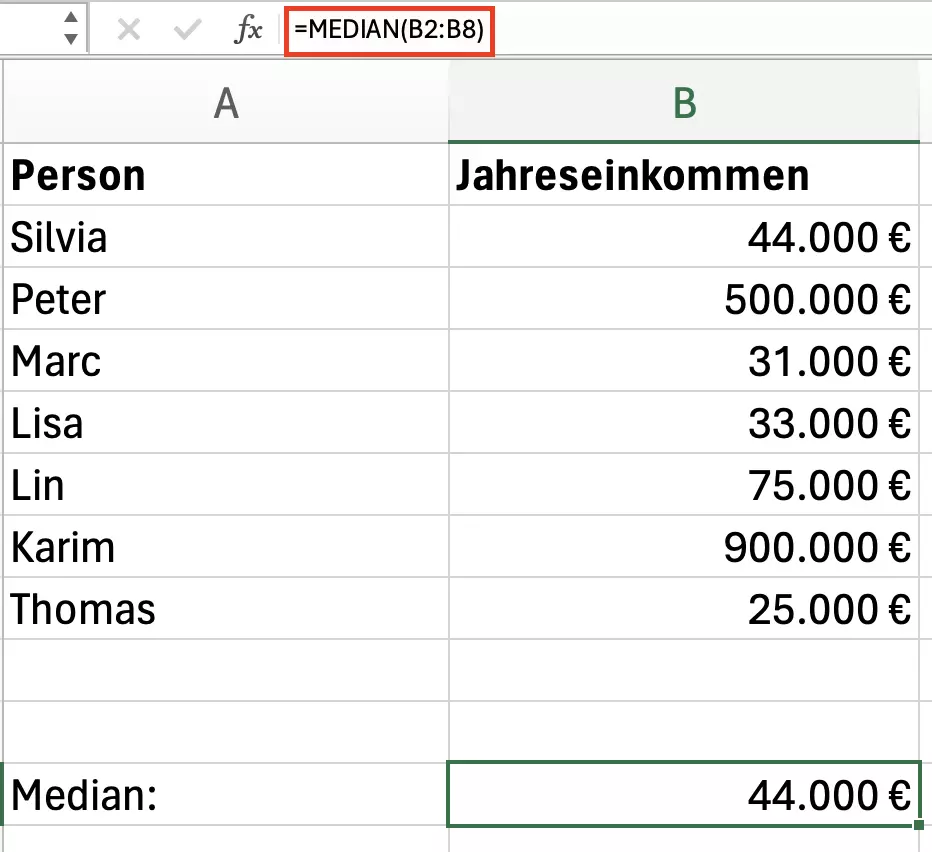
Der Median gibt die Mitte der Einkommensverhältnisse, also das Jahreseinkommen eines „normalen“ Angestellten, konkret wieder. Der Mittelwert hingegen läge in diesem Fall bei 229.714 € durchschnittlichem Jahreseinkommen, was als verfälschtes Einkommensverhältnis verstanden werden kann.
Bei einer ungleichmäßigen Gruppe von neun Personen wird der Median jeweils aus dem Durchschnitt des Unter- und Obermedians (hier: B3 und B6) ermittelt:
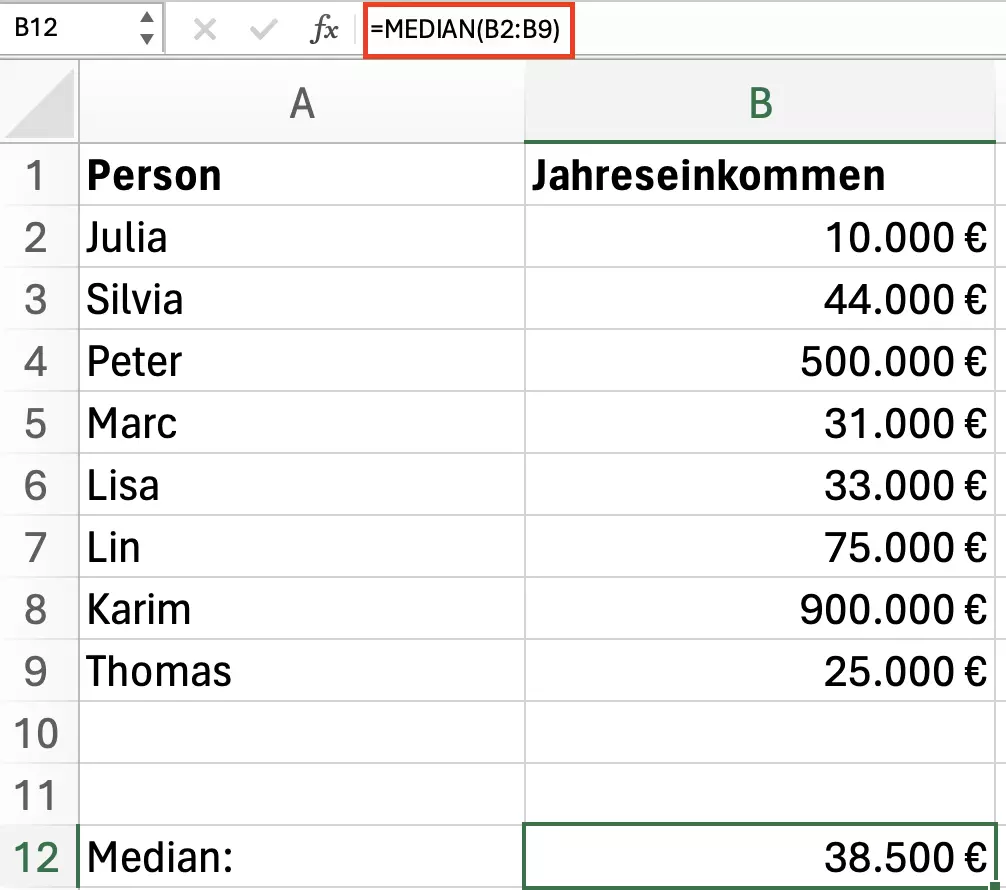
Beispiel 2: Median eines Notenspiegels
Bei der Ermittlung der zentralen Tendenz eines Notenspiegels hilft der Medien dabei, die Mitte einer nach Größe geordneten Notengruppe zu berechnen:
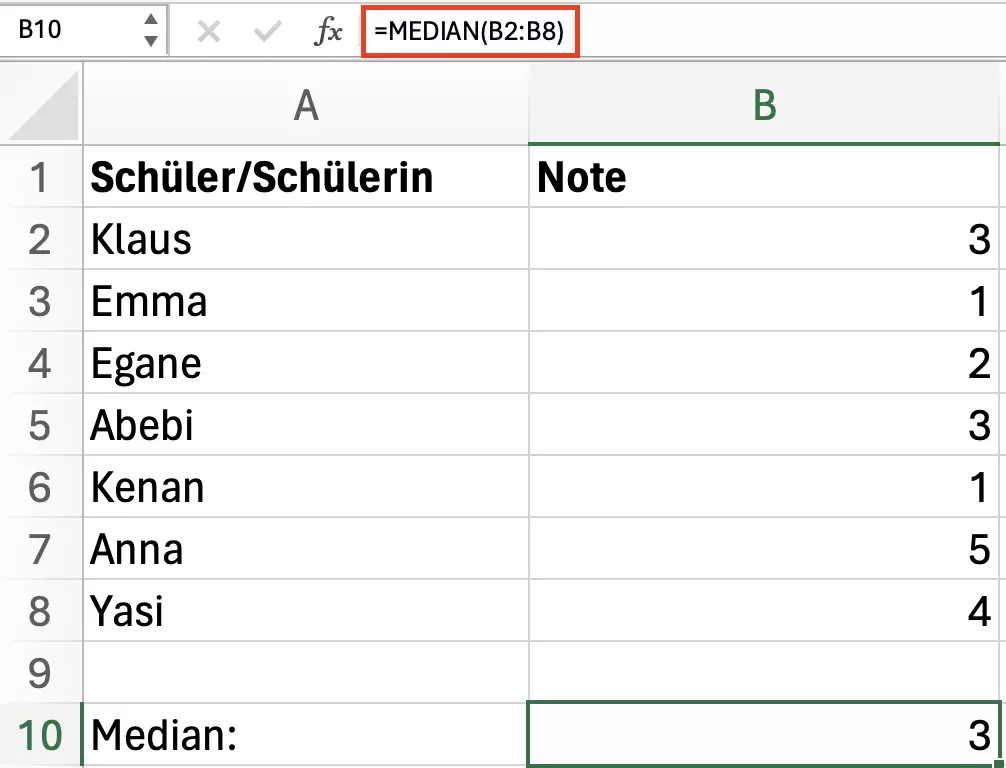
Auch ohne die praktische Hilfe von Excel lässt sich der Median berechnen. Hierbei gilt es die Zahlen einer Gruppe nach aufsteigender Größe zu ordnen und die mittlere Zahl (bei ungerader Anzahl) bzw. den Durchschnitt der zwei mittleren Zahlen (bei gerader Anzahl) zu ermitteln
- Daten zentral speichern, teilen und bearbeiten
- Serverstandort Deutschland (ISO 27001-zertifiziert)
- Höchste Datensicherheit im Einklang mit der DSGVO

