UTF-8: Der Standard im Netz
„UTF-8“ ist die Abkürzung für „8-Bit UCS Transformation Format“ und steht für die am weitesten verbreitete Zeichencodierung im World Wide Web. Der internationale Standard Unicode erfasst sämtliche Sprachzeichen und Textelemente (nahezu) aller Sprachen der Welt für die EDV-Verarbeitung. UTF-8 spielt im Unicode-Zeichensatz eine tragende Rolle.
- Intuitives Baukastensystem mit KI-Unterstützung
- Bilder und Texte wie von Profis gemacht, direkt SEO-optimiert
- Domain, SSL und E-Mail-Postfach inklusive
Die Entwicklung der UTF-8-Codierung
UTF-8 ist eine Zeichencodierung. Sie ordnet jedem existierenden Unicode-Zeichen genau eine bestimmte Bitfolge zu, die man auch als binäre Zahl lesen kann. Das heißt: Allen Buchstaben, Zahlen und Symbolen einer wachsenden Zahl an Sprachen weist UTF-8 jeweils eine feste, binäre Zahl zu. Internationale Organisationen, für die Internet-Standards von Bedeutung sind und die sie entsprechend etablieren wollen, arbeiten daran, UTF-8 zur unumstößlichen Größe bei der Codierung zu machen. Unter anderem das W3C sowie die Internet Engineering Task Force (IETF) setzen sich dafür ein. Und tatsächlich verwendeten bereits im Jahr 2009 die meisten Websites auf der Welt die UTF-8-Codierung. Im April 2025 nutzten laut einem W3Techs-Gutachten 98,6 Prozent aller existierenden Websites diese Zeichencodierung.
Probleme vor der Einführung von UTF-8
Verschiedene Regionen mit verwandten Sprachen und Schriftsystemen haben jeweils ihre eigenen Codierungsstandards entwickelt, da sie unterschiedliche Ansprüche hatten. Im englischsprachigen Raum genügte zum Beispiel die Codierung ASCII, deren Struktur die Zuordnung von 128 Zeichen zu einer computerlesbaren Zeichenkette zulässt.
Asiatische Schriften oder das kyrillische Alphabet nutzen jedoch mehr eindeutige Einzelzeichen. Auch die deutschen Umlaute (etwa der Buchstabe ä) fehlen bei ASCII. Zudem konnten sich Zuweisungen unterschiedlicher Codierungen doppeln. Dies führte dazu, dass beispielsweise ein in Russisch verfasstes Dokument auf einem amerikanischen Computer statt mit kyrillischen Buchstaben mit den auf diesem System zugewiesenen lateinischen Buchstaben dargestellt wurde. Das resultierende Kauderwelsch erschwerte die internationale Kommunikation erheblich.
Entstehung von UTF-8
Um dieses Problem zu lösen, entwickelte Joseph D. Becker für Xerox zwischen 1988 und 1991 den universellen Zeichensatz Unicode. Ab 1992 war auch das IT-Industriekonsortium X/Open auf der Suche nach einem System, das ASCII ablösen und das Zeichenrepertoire erweitern sollte. Trotzdem sollte die Codierung zu ASCII kompatibel bleiben.
Diese Anforderung erfüllte die erste Codierung namens UCS-2 nicht, da sie die Zeichennummern einfach in 16-Bit-Werte übertrug. Auch UTF-1 scheiterte, weil die Unicode-Zuweisungen mit den bestehenden ASCII-Zeichenzuweisungen teilweise kollidierten. Ein Server, der auf ASCII eingestellt war, gab dadurch teilweise falsche Zeichen aus. Das war ein erhebliches Problem, da zu dieser Zeit die Mehrheit der englischsprachigen Rechner damit arbeitete.
Der nächste Vorstoß bestand im File System Safe UCS Transformation Format (FSS-UTF) von Dave Prosser, das die Überlappung mit ASCII-Zeichen beseitigte. Im August desselben Jahres machte der Entwurf in Fachkreisen die Runde. In den Bell Labs, bekannt für zahlreiche Nobelpreisträger, arbeiteten damals die Unix-Mitbegründer Ken Thompson und Rob Pike am Betriebssystem Plan 9. Sie griffen Prossers Idee auf, entwickelten eine selbstsynchronisierende Codierung (jedes Zeichen gibt also an, wie viele Bits es benötigt) und legten Regeln für die Zuweisung von Buchstaben fest, die im Code unterschiedlich dargestellt werden konnten (Beispiel: „ä“ als eigenes Zeichen oder „a+¨“). Sie nutzten die Codierung erfolgreich für ihr Betriebssystem und stellten sie den Verantwortlichen vor. Damit war FSS-UTF, heute als „UTF-8“ bekannt, im Wesentlichen fertiggestellt.
UTF-8 im Unicode-Zeichensatz: Ein Standard für alle Sprachen
Die UTF-8-Codierung ist ein Transformationsformat innerhalb des Standards Unicode. Die internationale Normung ISO 10646 legt Unicode, dort unter der Bezeichnung „Universal Coded Character Set“, in weiten Teilen fest. Die Unicode-Entwickelnden grenzen gewisse Parameter für die praktische Anwendung ein. Der Standard soll die international einheitliche und kompatible Codierung von Schriftzeichen und Textelementen sicherstellen.
Bei seiner Einführung im Jahr 1991 legte Unicode 24 moderne Schriftsysteme sowie Währungszeichen für die Datenverarbeitung fest. Im 2024 veröffentlichten Unicode-Standard waren es 168. Es gibt verschiedene Unicode-Transformationsformate, kurz „UTF“, welche die 1.114.112 möglichen Codepoints reproduzieren. Drei Formate haben sich durchgesetzt: UTF-8, UTF-16 und UTF-32. Andere Codierungen wie UTF-7 oder SCSU haben zwar auch ihre Vorteile, konnten sich aber trotzdem nicht etablieren. Unicode ist in 17 Ebenen untergliedert, die jeweils 65.536 Zeichen umfassen. Eine Ebene besteht aus je 16 Spalten und Zeilen. Die nullte Ebene, die „Basic Multilingual Plane“, umfasst einen Großteil der aktuell auf der Welt genutzten Schriftsysteme sowie Satzzeichen, Kontrollzeichen und Symbole. Sechs weitere Ebenen werden derzeit verwendet:
- Supplementary Multilingual Plane (Ebene 1): historische Schriftsysteme, selten genutzte Zeichen
- Supplementary Ideographic Plane (Ebene 2): seltene CJK-Schriftzeichen („Chinesisch, Japanisch, Koreanisch“)
- Tertiary Ideographic Plane (Ebene 3): Seit der Unicode-Version 15.1 werden hier weitere CJK-Schriftzeichen kodiert.
- Supplementary Special-Purpose Plane (Ebene 14): einzelne Kontrollzeichen
- Supplementary Private Use Area – A (Ebene 15): private Nutzung
- Supplementary Private Use Area – B (Ebene 16): private Nutzung
Die UTF-Codierungen gewähren Zugriff auf alle Unicode-Zeichen. Die jeweiligen Eigenschaften empfehlen sich für bestimmte Einsatzbereiche.
Die Alternativen: UTF-32 und UTF-16
UTF-32 arbeitet immer mit 32 Bit, also 4 Byte. Die simple Struktur erhöht die Lesbarkeit des Formats. In Sprachen, die vornehmlich das lateinische Alphabet und somit nur die ersten 128 Zeichen nutzen, nimmt die Codierung sehr viel mehr Speicherplatz ein als nötig (4 statt 1 Byte).
UTF-16 etablierte sich als Darstellungsformat in Betriebssystemen wie Apple macOS und Microsoft Windows. In vielen Software-Entwicklungs-Frameworks findet es ebenso Anwendung. Es ist eines der ältesten UTFs, die noch immer genutzt werden. Seine Struktur eignet sich besonders für die speicherplatzsparende Codierung nichtlateinischer Sprachzeichen. Die meisten Zeichen lassen sich in 2 Byte (16 Bit) darstellen, nur bei seltenen Zeichen verdoppelt sich die Länge auf 4 Byte.
Effizient und skalierbar: UTF-8
UTF-8 besteht aus bis zu vier Bit-Ketten, die jeweils aus 8 Bits bestehen. Der Vorgänger ASCII besteht hingegen aus einer Bit-Kette mit 7 Bits. Beide Codierungen legen die ersten 128 codierten Zeichen deckungsgleich fest. Die hauptsächlich aus dem englischen Sprachraum stammenden Zeichen sind damit jeweils mit einem Byte abgedeckt. Für Sprachen mit lateinischem Alphabet nutzt dieses Format den Speicherplatz am effizientesten. Die Betriebssysteme Unix und Linux verwenden es intern. Seine bedeutendste Rolle spielt UTF-8 jedoch im Zusammenhang mit Internetanwendungen, nämlich bei der Darstellung von Text im World Wide Web oder in E-Mails.
Dank der selbstsynchronisierenden Struktur bleibt die Lesbarkeit trotz der variablen Länge pro Zeichen erhalten. Ohne Unicode-Einschränkung wären mit UTF-8 4.398.046.511.104 Zeichenzuordnungen möglich. Wegen der 4-Byte-Begrenzung in Unicode sind es effektiv 221, was mehr als ausreichend ist. Selbst der Unicode-Bereich hat noch leere Ebenen für viele weitere Schriftsysteme. Die genaue Zuordnung verhindert Codepoint-Überschneidungen, welche die Kommunikation in der Vergangenheit einschränkten.
Während UTF-16 und UTF-32 ebenso eine genaue Zuordnung ermöglichen, nutzt UTF-8 den Speicherplatz beim lateinischen Schriftsystem besonders effizient und ist darauf ausgelegt, dass verschiedene Schriftsysteme problemlos nebeneinander existieren können und abgedeckt werden. Dies ermöglicht deren gleichzeitige, sinnvolle Darstellung innerhalb eines Textfelds ohne Kompatibilitätsprobleme.
Grundlagen: UTF-8-Codierung und Zusammensetzung
Die Codierung UTF-8 besticht zum einen durch die Rückwärtskompatibilität zu ASCII und zum anderen durch eine selbstsynchronisierende Struktur, die es Entwicklerinnen und Entwicklern erleichtert, im Nachhinein Fehlerquellen auszumachen. Für sämtliche ASCII-Zeichen nutzt UTF nur 1 Byte. Die Gesamtzahl der Bit-Ketten ist an den ersten Ziffern der binären Zahl zu erkennen. Da der ASCII-Code nur 7 Bits umfasst, ist die vorderste Ziffer die Kennziffer 0. Die 0 füllt den Speicherplatz auf ein volles Byte und signalisiert den Start einer Kette ohne Folgeketten. Der Name „UTF-8“ würde als binäre Zahl mit UTF-8-Codierung beispielsweise wie folgt ausgedrückt:
| Zeichen | U | T | F | - | 8 |
|---|---|---|---|---|---|
| UTF-8, binär | 01010101 | 01010100 | 01010100 | 00101101 | 00111000 |
| Unicode-Point, hexadezimal | U+0055 | U+0054 | U+0046 | U+002D | U+0038 |
ASCII-Zeichen wie die in der Tabelle verwendeten ordnet die UTF-8-Codierung einer einzelnen Bit-Kette zu. Alle folgenden Zeichen und Symbole innerhalb des Unicodes haben zwei bis vier 8-Bit-Ketten. Die erste Kette nennt sich Start-Byte, zusätzliche Ketten sind Folge-Bytes. Start-Bytes mit Folge-Bytes beginnen immer mit 11. Folge-Bytes hingegen beginnen immer mit 10. Suchen Sie manuell nach einem bestimmten Punkt im Code, erkennen Sie daher den Anfang eines codierten Zeichens durch die Marker 0 und 11. Das erste druckbare Mehr-Byte-Zeichen ist das umgekehrte Ausrufezeichen:
| Zeichen | ¡ |
|---|---|
| UTF-8, binär | 11000010 10100001 |
| Unicode-Point, hexadezimal | U+00A1 |
Die Präfix-Codierung verhindert, dass innerhalb einer Byte-Kette ein weiteres Zeichen codiert wird. Fängt ein Byte-Strom in der Mitte eines Dokuments an, stellt der Computer trotzdem die lesbaren Zeichen richtig dar, da er unvollständige erst gar nicht abbildet. Suchen Sie nach dem Anfang eines Zeichens, bedingt die 4-Byte-Grenze, dass Sie an einem beliebigen Punkt höchstens drei Byte-Ketten zurückgehen müssen, um das Start-Byte zu finden.
Ein weiteres strukturierendes Element: Die Anzahl der Einsen am Anfang des Start-Bytes kennzeichnet die Länge der Byte-Kette:
110xxxxxsteht für 2 Byte1110xxxxsteht für 3 Byte11110xxxsteht für 4 Byte
In Unicode entspricht der zugeordnete Byte-Wert der Zeichennummer, was eine lexikalische Ordnung ermöglicht. Es gibt jedoch Lücken. Der Unicode-Bereich U+007F bis U+009F umfasst nicht sichtbare Kontrollzahlen. Der UTF-8-Standard ordnet dort keine druckbaren Zeichen zu, nur Kommandos.
Die UTF-8-Codierung kann, wie erwähnt, theoretisch bis zu acht Byte-Ketten aneinanderreihen. Unicode schreibt jedoch eine Länge von höchstens 4 Byte vor. Das hat zum einen die Folge, dass Byte-Ketten mit 5 Byte oder mehr standardmäßig ungültig sind. Zum anderen reflektiert diese Einschränkung das Bestreben, Code möglichst kompakt – also mit wenig Speicherplatzbelastung – und möglichst strukturiert abzubilden. So lautet eine grundsätzliche Regel bei der Verwendung von UTF-8, dass immer die kürzestmögliche Codierung genutzt werden soll.
Diese Regel ist der Grund, dass die mit 192 und 193 beginnenden Byte-Folgen unzulässig sind. Denn sie stellen potenziell Zeichen im ASCII-Bereich (0–127) mit 2 Byte dar, die bereits mit 1 Byte codiert sind.
Für manche Zeichen gibt es jedoch mehrere gleichwertige Kodierungen. Der Buchstabe ä wird beispielsweise mittels 2 Bytes codiert: 11000011 10100100. Theoretisch ist es möglich, die Codepoints für den Buchstaben „a“ (01100001) und das Diäresis-Zeichen „*“ (11001100 10001000) zu kombinieren, um „ä“ darzustellen: 01100001 11001100 10001000. Hier wird die sogenannte Unicode-Normalisierungsform NFD genutzt, bei der Zeichen kanonisch dekomponiert werden. Beide gezeigten Kodierungen führen zum exakt selben Ergebnis (nämlich „ä“) und sind daher kanonisch äquivalent.
Normalisierungen dienen dazu, unterschiedliche Unicode-Darstellungen desselben Zeichens zu vereinheitlichen. Dabei ist kanonische Äquivalenz wichtig: Sie besagt, dass zwei Zeichenfolgen zwar unterschiedlich kodiert sein können, aber dieselbe Bedeutung und Darstellung haben. Kompatible Äquivalenz hingegen erlaubt auch Zeichenfolgen, die sich in Format oder Stil unterscheiden, aber inhaltlich gleich sind. Die Unicode-Normalisierungsformen (z. B. NFC, NFD, NFKC, NFKD) nutzen diese Konzepte, um Texte zu standardisieren. So wird sichergestellt, dass Vergleiche, Sortierungen und Suchen konsistent und zuverlässig funktionieren.
Einige Unicode-Wertebereiche wurden für UTF-8 nicht definiert, da sie für UTF-16-Surrogates bereitstehen. Die Übersicht zeigt, welche Bytes in UTF-8 unter Unicode laut Internet Engineering Task Force (IETF) als zulässig gelten (grün markierte Bereiche sind gültige Bytes, orange markierte sind ungültige).
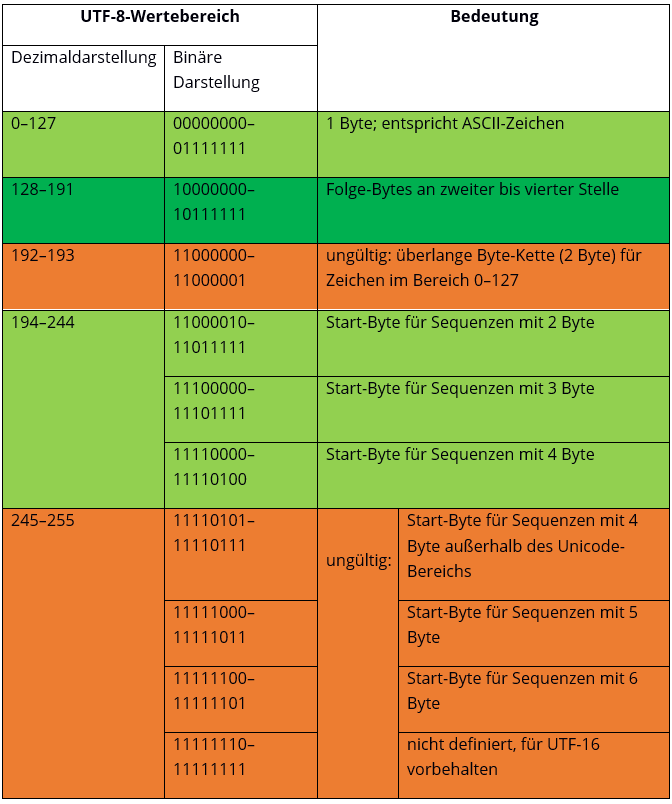
Umrechnung von Unicode hexadezimal zu UTF-8 binär
Computer lesen nur binäre Zahlen, Menschen nutzen ein Dezimalsystem. Eine Schnittstelle zwischen diesen Formen ist das Hexadezimalsystem. Es hilft dabei, lange Bit-Ketten kompakt darzustellen. Es verwendet die Ziffern 0 bis 9 und die Buchstaben A bis F und agiert auf der Basis der Zahl 16. Als vierte Potenz von 2 eignet sich das Hexadezimalsystem besser als das Dezimalsystem dafür, achtstellige Byte-Bereiche darzustellen.
Eine Hexadezimalziffer steht für eine Viererkette („Nibble“) innerhalb des Oktetts. Ein Byte mit acht Binärziffern kann also mit nur zwei Hexadezimalziffern dargestellt werden. Unicode nutzt das Hexadezimalsystem dafür, die Position eines Zeichens innerhalb des eigenen Systems zu beschreiben. Daraus lassen sich die binäre Zahl und schließlich der UTF-8-Codepoint errechnen.
Zuerst muss die Binärzahl aus der Hexadezimalzahl umgewandelt werden. Dann passen Sie die Codepoints in die Struktur der UTF-8-Codierung ein. Um sich die Strukturierung zu erleichtern, nutzen Sie folgende Übersicht, die zeigt, wie viele Codepoints in eine Byte-Kette passen und welche Struktur Sie in welchem Unicode-Wertebereich zu erwarten haben.
| Größe in Byte | freie Bits zur Bestimmung | erster Unicode-Codepoint | letzter Unicode-Codepoint | Start-Byte / Byte 1 | Folge-Byte 2 | Folge-Byte 3 | Folge-Byte 4 |
|---|---|---|---|---|---|---|---|
| 1 | 7 | U+0000 | U+007F | 0xxxxxxx | |||
| 2 | 11 | U+0080 | U+07FF | 110xxxxx | 10xxxxxx | ||
| 3 | 16 | U+0800 | U+FFFF | 1110xxxx | 10xxxxxx | 10xxxxxx | |
| 4 | 21 | U+10000 | U+10FFFF | 11110xxx | 10xxxxxx | 10xxxxxx | 10xxxxxx |
Innerhalb eines Code-Bereichs können Sie eine Anzahl verwendeter Bytes voraussetzen, da die lexikalische Ordnung bei der Nummerierung der Unicode-Codepoints und UTF-8-Binärzahlen eingehalten wird. Innerhalb des Bereiches U+0800 und U+FFFF nutzt UTF-8 also 3 Bytes. Es stehen 16 Bits dafür zur Verfügung, den Codepoint eines Symbols auszudrücken. Die Einordnung einer errechneten Binärzahl in das UTF-8-Schema erfolgt von rechts nach links, wobei Sie etwaige Leerstellen links mit Nullen auffüllen.
Beispielrechnung:
Das Zeichenᅢ(Hangul Junseong, Ä) steht in Unicode an Stelle U+1162. Um die Binärzahl zu berechnen, wandeln Sie zuerst die Hexadezimalzahl in eine Dezimalzahl um. Jede Stelle in der Zahl entspricht der korrelierenden Potenz von 16. Die rechte Ziffer hat dabei den niedrigsten Wert mit 160 = 1. Von rechts beginnend, multiplizieren Sie den Zahlenwert der Ziffer mit dem der Potenz. Anschließend addieren Sie die Ergebnisse.
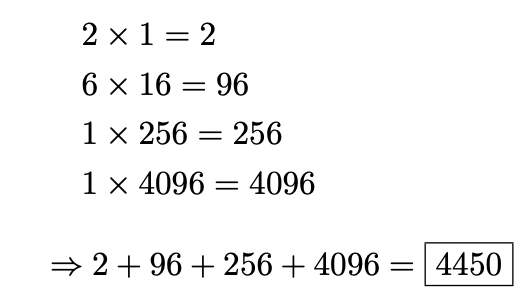
4450 ist die berechnete Dezimalzahl. Diese wandeln Sie nun in eine Binärzahl um. Dazu teilen Sie die Zahl so lange mit Rest durch 2, bis das Ergebnis 0 ist. Der Rest, von rechts nach links aufgeschrieben, ist die Binärzahl.
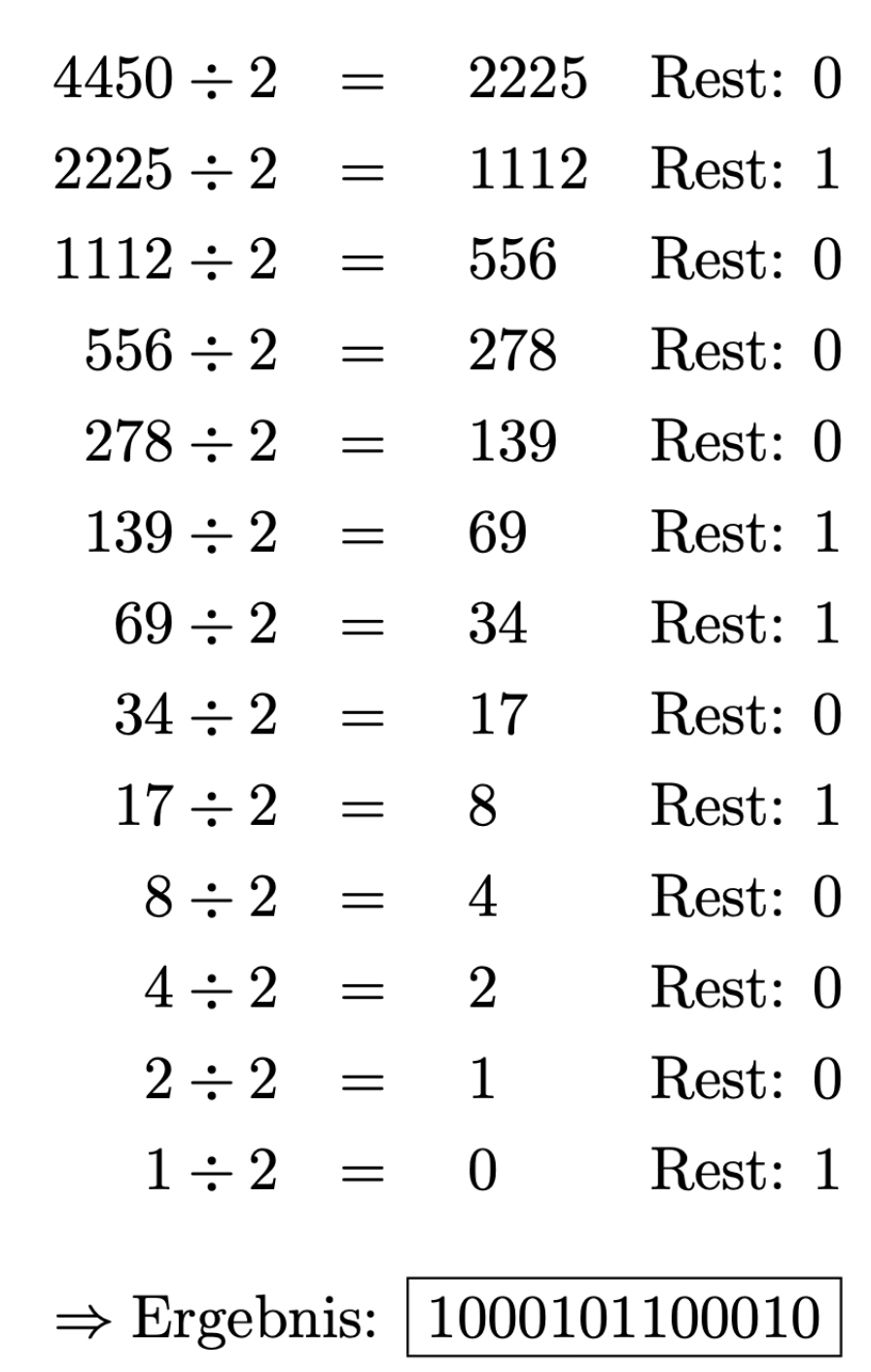
Der UTF-8-Code schreibt für den Codepoint U+1162 3 Bytes vor, denn der Codepoint liegt zwischen U+0800 und U+FFFF. Das Start-Byte beginnt also mit 1110. Die zwei Folge-Bytes beginnen jeweils mit 10. Die Binärzahl ergänzen Sie in den freien Bits, die nicht die Struktur vorgeben, von rechts nach links. Übrige Bit-Stellen im Start-Byte ergänzen Sie mit 0, bis das Oktett voll ist. Die UTF-8-Codierung sieht dann so aus:
11100001 10000101 10100010 (der eingefügte Codepoint ist gefettet)
| Zeichen | Unicode-Codepoint, hexadezimal | Dezimalzahl | Binärzahl | UTF-8 |
|---|---|---|---|---|
| ᅢ | U+1162 | Dezimalzahl | 4450 | 1000101100010 |
UTF-8 im Editor
UTF-8 ist zwar der am weitesten verbreitete Standard im Internet, einfache Text-Editoren speichern Texte aber nicht unbedingt standardmäßig in diesem Format ab. Microsoft Notepad nutzt beispielsweise standardmäßig eine Codierung, die es als „ANSI“ bezeichnet (dahinter verbirgt sich die ASCII-basierte Codierung „Windows-1252“). Wollen Sie eine Text-Datei aus Microsoft Word heraus in UTF-8 konvertieren (zum Beispiel, um verschiedene Schriftsysteme abzubilden), gehen Sie wie folgt vor: Gehen Sie auf „Speichern unter“ und wählen Sie unter Dateityp die Option „Nur Text“.
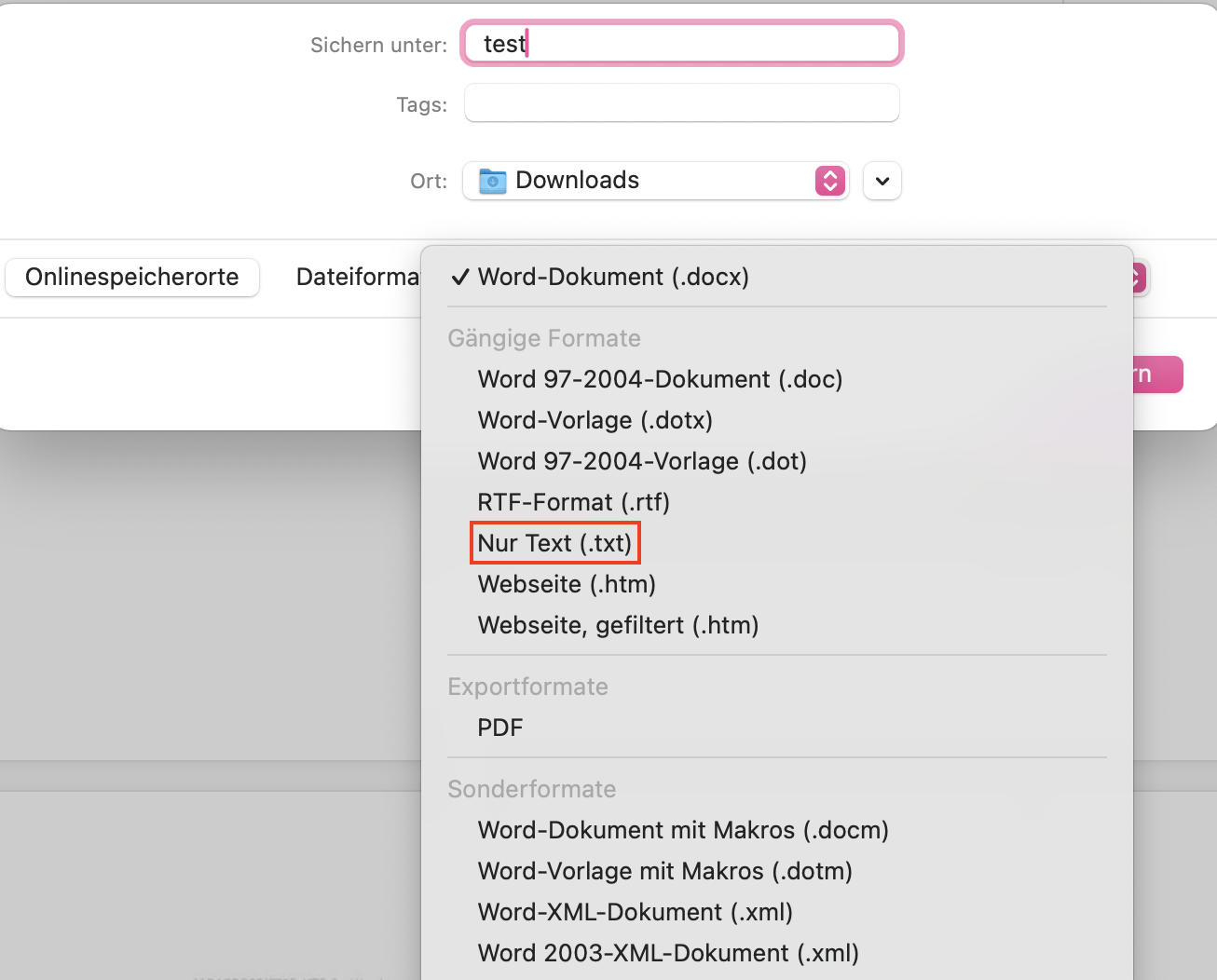
Das Pop-up-Fenster „Dateikonvertierung“ öffnet sich. Wählen Sie unter „Textcodierung“ den Punkt „Andere Codierung“ und aus der Liste die Option „Unicode (UTF-8)“. Im Drop-down-Menü „Zeilen beenden mit“ wählen Sie „Wagenrücklauf/Zellenvorschub“ beziehungsweise „CR/LF“. So einfach konvertieren Sie eine Datei in den Unicode-Zeichensatz mit UTF-8.
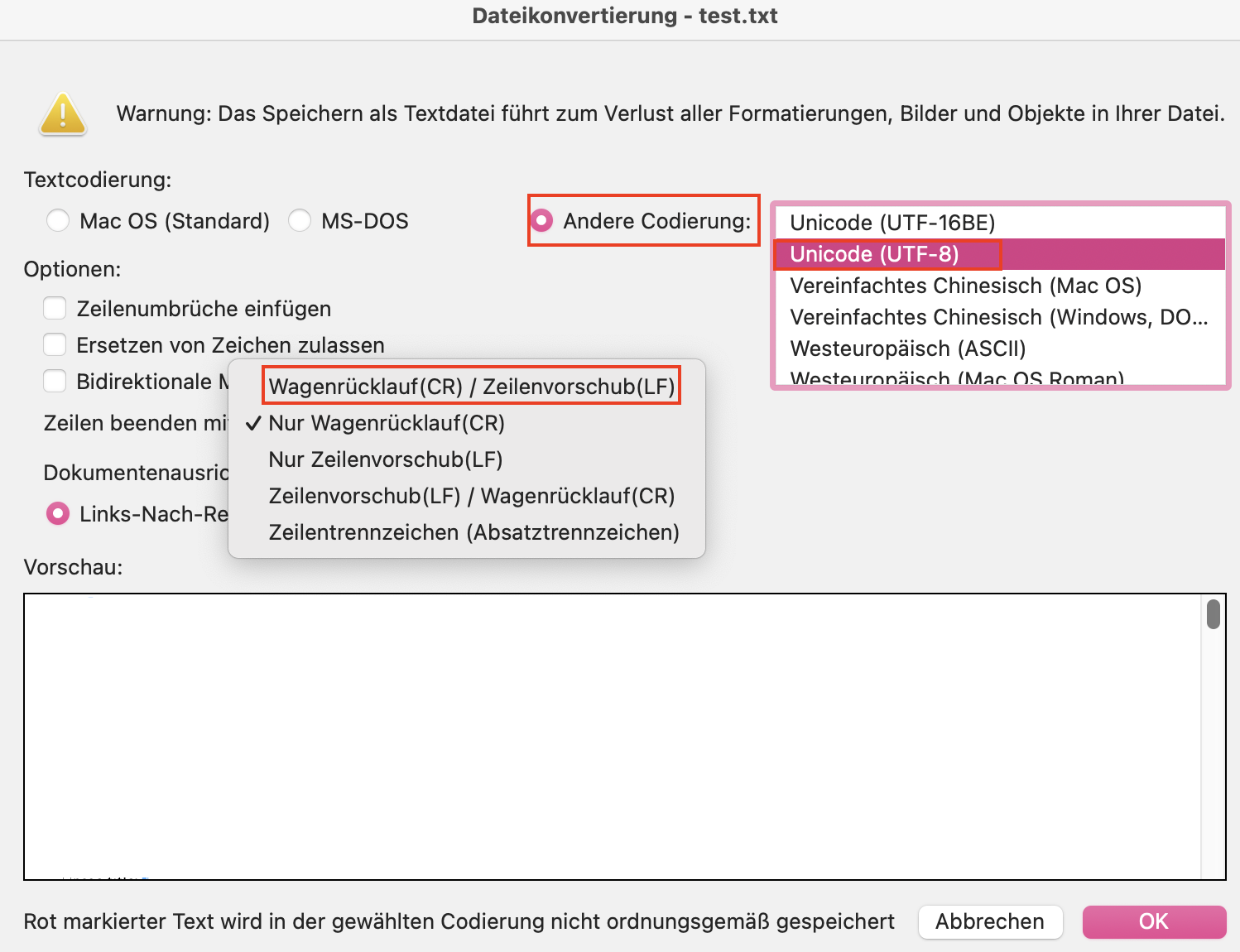
Öffnen Sie eine unmarkierte Text-Datei, bei der Sie vorher nicht wissen, welche Codierung angewendet wurde, kann es bei der Bearbeitung zu Problemen kommen. Unter Unicode nutzt man für solche Gelegenheiten die Byte Order Mark (BOM). Mit diesem unsichtbaren Zeichen lässt sich anzeigen, ob das Dokument in einem Big-Endian- oder Little-Endian-Format vorliegt. Wenn nämlich ein Programm eine Datei in UTF-16 Little-Endian mithilfe von UTF-16 Big-Endian decodiert, wird der Text fehlerhaft ausgegeben.
Dokumente, die auf dem UTF-8-Zeichensatz aufbauen, haben dieses Problem nicht, da die Byte-Reihenfolge immer als Big-Endian-Byte-Sequenz ausgelesen wird. Die BOM dient in diesem Fall lediglich als Hinweis darauf, dass das vorliegende Dokument UTF-8-codiert ist.
Zeichen, die mit mehr als einem Byte dargestellt werden, können in manchen Codierungen (UTF-16 und UTF-32) das höchstwertige Byte an vorderster (links) oder hinterster (rechts) Position besitzen. Steht das höchstwertige Byte („Most Significant Byte“, MSB) vorne, erhält die Codierung den Zusatz „Big-Endian“, steht das MSB hinten, wird „Little-Endian“ angefügt.
Sie setzen die BOM vor einen Datenstrom beziehungsweise an den Anfang einer Datei. Die Markierung hat Vorrang vor allen anderen Anweisungen, auch vor dem HTTP-Header. Die BOM dient als eine Art Signatur für Unicode-Codierungen und hat den Codepoint U+FEFF. Je nachdem, welche Codierung benutzt wird, stellt sich die BOM in der codierten Form unterschiedlich dar.
| Codierungsformat | BOM, Codepoint: U+FEFF (hex.) |
|---|---|
| UTF-8 | EF BB BF |
| UTF-16 Big-Endian | FE FF |
| UTF-16 Little-Endian | FF FE |
| UTF-32 Big-Endian | 00 00 FE FF |
| UTF-32 Little-Endian | FF FE 00 00 |
Die Byte Order Mark verwenden Sie nicht, wenn das Protokoll es explizit verbietet oder Ihre Daten bereits einem bestimmten Typ zugeordnet sind. Manche Programme erwarten laut Protokoll ASCII-Zeichen. Da UTF-8 rückwärtskompatibel mit der ASCII-Codierung ist und seine Byte-Reihenfolge feststeht, brauchen Sie dann keine BOM. Tatsächlich empfiehlt Unicode, die BOM unter UTF-8 nicht zu nutzen. Da sie aber in älterem Code vorkommen und Probleme bereiten kann, ist es wichtig, die eventuell vorhandene BOM als solche zu identifizieren.
- Professionelle Templates
- Änderungen am Design mit nur einem Klick
- Domain, SSL und E-Mail-Postfach inklusive

